General Applications of Neural Networks
Session 2: Feed Forward Neural Networks

Instructor: Wesley Beckner

Contact: wesleybeckner@gmail.com

---

In this session we will continue with our discussion on neural networks. Specifically, we will revisit the concept of learning curves, regularization and classification tasks, this time as they pertain to neural networks!

images in this notebook borrowed from Ryan Holbrook

---

2.0 Preparing Environment and Importing Data

back to top

!pip uninstall scikit-learn -y

!pip install -U scikit-learn

Found existing installation: scikit-learn 0.22.2.post1
Uninstalling scikit-learn-0.22.2.post1:
  Successfully uninstalled scikit-learn-0.22.2.post1
Collecting scikit-learn
  Downloading scikit_learn-0.24.2-cp37-cp37m-manylinux2010_x86_64.whl (22.3 MB)
     |████████████████████████████████| 22.3 MB 2.2 MB/s 
[?25hRequirement already satisfied: numpy>=1.13.3 in /usr/local/lib/python3.7/dist-packages (from scikit-learn) (1.19.5)
Collecting threadpoolctl>=2.0.0
  Downloading threadpoolctl-2.2.0-py3-none-any.whl (12 kB)
Requirement already satisfied: scipy>=0.19.1 in /usr/local/lib/python3.7/dist-packages (from scikit-learn) (1.4.1)
Requirement already satisfied: joblib>=0.11 in /usr/local/lib/python3.7/dist-packages (from scikit-learn) (1.0.1)
Installing collected packages: threadpoolctl, scikit-learn
Successfully installed scikit-learn-0.24.2 threadpoolctl-2.2.0

2.0.1 Import Packages

back to top

from tensorflow import keras
from tensorflow.keras import layers
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import tensorflow as tf
from copy import copy
import numpy as np
sns.set()

from sklearn.preprocessing import StandardScaler, OneHotEncoder, LabelEncoder
from sklearn.compose import make_column_transformer, make_column_selector
from sklearn.metrics import classification_report,confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn import set_config
from sklearn.pipeline import make_pipeline
from sklearn.impute import SimpleImputer
set_config(display='diagram')

2.0.2 Load Dataset

back to top

wine = pd.read_csv("https://raw.githubusercontent.com/wesleybeckner/"\
      "ds_for_engineers/main/data/wine_quality/winequalityN.csv")

# create X and y
X = wine.copy()
y = X.pop('quality')

# split into train/test
X_train, X_test, y_train, y_test = train_test_split(X, y)
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train)

# the numerical values pipe
num_proc = make_pipeline(SimpleImputer(strategy='median'), StandardScaler())

# the categorical values pipe
cat_proc = make_pipeline(
    SimpleImputer(strategy='constant', fill_value='missing'),
    OneHotEncoder(handle_unknown='ignore'))

# parallelize the two pipes
preprocessor = make_column_transformer((num_proc,
                                make_column_selector(dtype_include=np.number)),
                                       (cat_proc,
                                make_column_selector(dtype_include=object)))

X_train_std = preprocessor.fit_transform(X_train) # fit_transform on train
X_test_std = preprocessor.transform(X_test) # transform test
X_val_std = preprocessor.transform(X_val)

y_train_std = np.log(y_train) # log output y
y_val_std = np.log(y_val) # log output y
y_test_std = np.log(y_test) # log output y

preprocessor

ColumnTransformer

ColumnTransformer(transformers=[('pipeline-1',
                                 Pipeline(steps=[('simpleimputer',
                                                  SimpleImputer(strategy='median')),
                                                 ('standardscaler',
                                                  StandardScaler())]),
                                 ),
                                ('pipeline-2',
                                 Pipeline(steps=[('simpleimputer',
                                                  SimpleImputer(fill_value='missing',
                                                                strategy='constant')),
                                                 ('onehotencoder',
                                                  OneHotEncoder(handle_unknown='ignore'))]),
                                 )])

pipeline-1

SimpleImputer

SimpleImputer(strategy='median')

StandardScaler

StandardScaler()

pipeline-2

SimpleImputer

SimpleImputer(fill_value='missing', strategy='constant')

OneHotEncoder

OneHotEncoder(handle_unknown='ignore')

2.1 Evaluating the Model

back to top

In the last session, we randomly chose 10 and then 30 epochs (10 rounds of the training data) to train our neural network. Now we'll garner the language to be more systematic in our approach.

2.1.1 Learning Curves

Recall learning curves from last week, where we plot model score (accuracy/mse/r2/etc.) over model complexity (trees in a forest, degrees in a polynomial, etc.):

img src

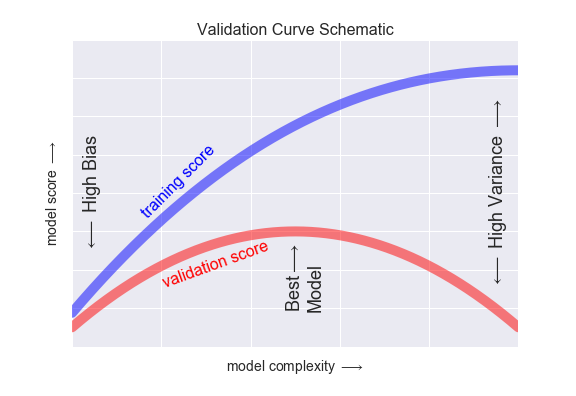
We have a similar situation with neural networks, accept here, the model complexity is defined by both the number of epochs, and the capacity of the model.

2.1.1.1 Training Data (Epochs)

A greater number of epochs allows the model to further tune itself to the training data. Remember that our model solves its weights by a solver function, most often a form of stochastic gradient descent. Because this solver is iterative, the longer we allow it run the closer it will get to finding its true weights. The caveat here is that, like we have seen before, the model is only learning the proper weights according to the training data, which we know includes noise, otherwise known as irreducible error. Our data science senses should be tingling: there's an optimum number of epochs here, and it will counter balance the trade-off between error due to bias (too few epochs) and error due to variance (too many epochs).

2.1.1.2 Complexity (Capacity)

The capacity of the model is defined by the architecture. It is the total number of trainable weights available to the solver function. The more weights, the more capacity. Capacity determines the upper limit for which our model can learn relationships between the data. Again we should recall from our session on feature engineering: the more training data we have, the more capacity we should give our model to account for that abundance of training data. This is also influenced by the actual complexity between the input and output data, X and y, who's function we are attempting to approximate with the neural network. The more complicated the relationship, the more capacity we should give to our model.

Capacity can be increased either by widening our model (increasing the neurons in a layer) or deepening our model(increasing the number of layers in our model).

2.1.2 Early Stopping

back to top

Without knowing the true relationship between X and y, or the degree to which there is irreducible error in our data, we return to our familiar learning curves to pragmaticaly determine how long we should train our model, that is, how many epochs should be ran and how many neurons we should give our model.

When dealing with the number of epochs, we can program this into the training session automatically with early stopping. Early stopping allows us to discontinue training the model when either the validation score stops improving, or stops improving by some margin. This allows us to both save time during training and to avoid overfitting our model.

To account for underfitting (not training the model long enough) we can simply set our number of training epochs to some large number and allow early stopping to take care of the rest.

In TF/Keras, we can envoke early stopping by setting a callback a callback is simply a function that is called every so often.

from tensorflow.keras.callbacks import EarlyStopping

early_stopping = EarlyStopping(
    min_delta=0.001, # minimium amount of change to count as an improvement
    patience=20, # how many epochs to wait before stopping
    restore_best_weights=True,
)

In the above, we are saying detect when the validation loss stops improving by 0.001; check this over the past 20 epochs to avoid stopping early due to noise; and restore the best weights over that past 20 epoch period when early stopping is envoked. To envoke early stopping we would enlist it in our call to fit like so:

model.fit(
    # X, y, batch size etc, ...
    callbacks=[early_stopping],
)

🏋️ Exercise 1: Try Early Stopping

Take your best model from the last exercise in session 1 and apply early stopping

from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.callbacks import EarlyStopping

model = keras.Sequential([
    ### YOUR CODE HERE ###
])

model.compile(
    optimizer='adam',
    loss='mse',
)

early_stopping = EarlyStopping(
    min_delta=0.001, # minimium amount of change to count as an improvement
    patience=20, # how many epochs to wait before stopping
    restore_best_weights=True,
)

print(model.summary())

history = model.fit(
    X_train_std, y_train_std,
    validation_data=(X_val_std, y_val_std),
    batch_size=256,
    epochs=1000,
    verbose=1,
    callbacks=[early_stopping],
)

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_5 (Dense)              (None, 32)                448       
_________________________________________________________________
dense_6 (Dense)              (None, 1024)              33792     
_________________________________________________________________
dense_7 (Dense)              (None, 1024)              1049600   
_________________________________________________________________
dense_8 (Dense)              (None, 32)                32800     
_________________________________________________________________
dense_9 (Dense)              (None, 1)                 33        
=================================================================
Total params: 1,116,673
Trainable params: 1,116,673
Non-trainable params: 0
_________________________________________________________________
None
Epoch 1/1000
15/15 [==============================] - 2s 50ms/step - loss: 0.4680 - val_loss: 0.1534
Epoch 2/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.1286 - val_loss: 0.0802
Epoch 3/1000
15/15 [==============================] - 1s 40ms/step - loss: 0.0770 - val_loss: 0.0502
Epoch 4/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0511 - val_loss: 0.0378
Epoch 5/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0362 - val_loss: 0.0321
Epoch 6/1000
15/15 [==============================] - 1s 40ms/step - loss: 0.0298 - val_loss: 0.0272
Epoch 7/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0268 - val_loss: 0.0288
Epoch 8/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0223 - val_loss: 0.0206
Epoch 9/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0190 - val_loss: 0.0204
Epoch 10/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0177 - val_loss: 0.0218
Epoch 11/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0166 - val_loss: 0.0185
Epoch 12/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0152 - val_loss: 0.0207
Epoch 13/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0153 - val_loss: 0.0197
Epoch 14/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0147 - val_loss: 0.0204
Epoch 15/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0143 - val_loss: 0.0178
Epoch 16/1000
15/15 [==============================] - 1s 40ms/step - loss: 0.0133 - val_loss: 0.0165
Epoch 17/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0124 - val_loss: 0.0168
Epoch 18/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0129 - val_loss: 0.0166
Epoch 19/1000
15/15 [==============================] - 1s 40ms/step - loss: 0.0128 - val_loss: 0.0159
Epoch 20/1000
15/15 [==============================] - 1s 40ms/step - loss: 0.0119 - val_loss: 0.0159
Epoch 21/1000
15/15 [==============================] - 1s 40ms/step - loss: 0.0115 - val_loss: 0.0159
Epoch 22/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0112 - val_loss: 0.0158
Epoch 23/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0113 - val_loss: 0.0161
Epoch 24/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0113 - val_loss: 0.0173
Epoch 25/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0105 - val_loss: 0.0160
Epoch 26/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0104 - val_loss: 0.0172
Epoch 27/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0107 - val_loss: 0.0160
Epoch 28/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0099 - val_loss: 0.0159
Epoch 29/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0096 - val_loss: 0.0153
Epoch 30/1000
15/15 [==============================] - 1s 51ms/step - loss: 0.0097 - val_loss: 0.0176
Epoch 31/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0103 - val_loss: 0.0180
Epoch 32/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0102 - val_loss: 0.0161
Epoch 33/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0095 - val_loss: 0.0173
Epoch 34/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0101 - val_loss: 0.0171
Epoch 35/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0102 - val_loss: 0.0176
Epoch 36/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0092 - val_loss: 0.0160
Epoch 37/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0090 - val_loss: 0.0158
Epoch 38/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0088 - val_loss: 0.0200
Epoch 39/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0110 - val_loss: 0.0189
Epoch 40/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0096 - val_loss: 0.0172
Epoch 41/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0093 - val_loss: 0.0151
Epoch 42/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0082 - val_loss: 0.0153
Epoch 43/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0075 - val_loss: 0.0167
Epoch 44/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0080 - val_loss: 0.0157
Epoch 45/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0079 - val_loss: 0.0152
Epoch 46/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0077 - val_loss: 0.0173
Epoch 47/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0088 - val_loss: 0.0161
Epoch 48/1000
15/15 [==============================] - 1s 41ms/step - loss: 0.0081 - val_loss: 0.0166
Epoch 49/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0080 - val_loss: 0.0195

# Show the learning curves
history_df = pd.DataFrame(history.history)
fig, ax = plt.subplots(1,1)
history_df.plot(ax=ax)
ax.set_ylim(0,.1)

(0.0, 0.1)

y_test_pred = np.exp(model.predict(X_test_std))
plt.plot(y_test_pred, np.exp(y_test_std), ls='', marker='o')

[<matplotlib.lines.Line2D at 0x7f4c409a6210>]

2.2 Regularizing Layers: Dropout and Batch Normalization

back to top

There are dozens of different layer types for accomplishing different tasks (and more are being generated by researchers all the time). While we're on the topic of general model performance, there are two layer types we'll want to introduce here: dropout and batch normalization or just batchnorm. What we'll see with both of these types is that while they don't contain any neurons, they're useful to think of as layers, because they are an extra processing step between neural layers.

2.2.1 Dropout

back to top

Dropout is the Neural Network response to the wide success of ensemble learning. In a dropout layer, random neurons are dropped in each batch of training, i.e. their weighted updates are not sent to the next neural layer. Just as with random forests, the end result is that the neural network can be thought of as many independent models that vote on the final output.

Put another way, when a network does not contain dropout layers, and has a capacity that exceeds that which would be suited for the true, underlying complexity level of the data, it can begin to fit to noise. This ability to fit to noise is based on very specific relationships between neurons, which fire uniquely given the particular training example. Adding dropout breaks these specific neural connections, and so the neural network as a whole is forced to find weights that apply generally, as there is no guarantee they will be turned on when their specific training example they would usually overfit for comes around again.

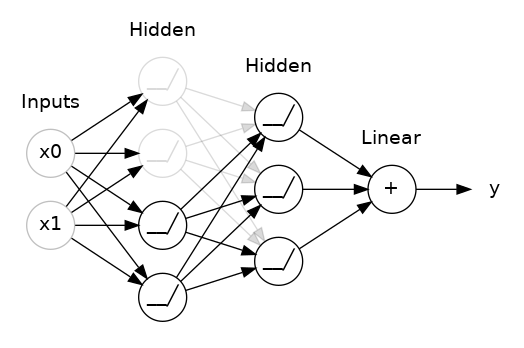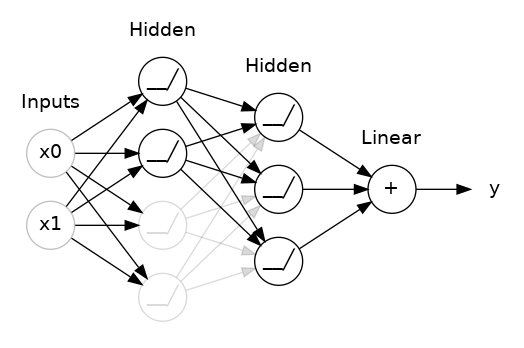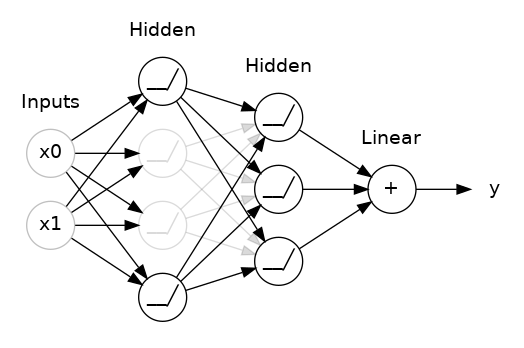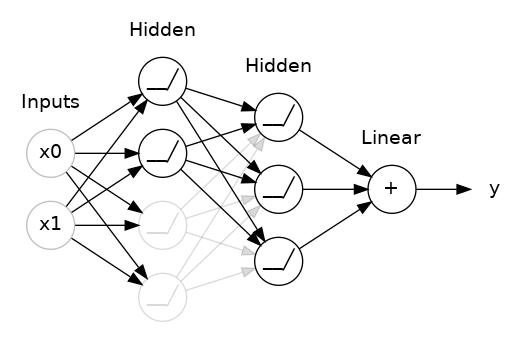
Network with 50% dropout

A last thing to note, is that after adding dropout, we will typically need to add additional layers to our network to maintain the overall capacity of the network.

keras.Sequential([
    # ...
    layers.Dropout(rate=0.3), # apply 30% dropout to the next layer
    layers.Dense(16),
    # ...
])

<tensorflow.python.keras.engine.sequential.Sequential at 0x7f2ae011ba50>

When adding dropout to a model we will usually want to increase the depth:

# Dropout model

model = keras.Sequential([
    layers.Dense(512, activation='relu', input_shape=[X_train_std.shape[1]]),
    layers.Dropout(0.3),
    layers.Dense(512*2, activation='relu'),
    layers.Dropout(0.3),
    layers.Dense(512, activation='relu'),
    layers.Dense(1),
])

model.compile(
    optimizer='adam',
    loss='mse',
)

early_stopping = EarlyStopping(
    min_delta=0.001, # minimium amount of change to count as an improvement
    patience=20, # how many epochs to wait before stopping
    restore_best_weights=True,
)

print(model.summary())

history = model.fit(
    X_train_std, y_train_std,
    validation_data=(X_val_std, y_val_std),
    batch_size=256,
    epochs=1000,
    verbose=1,
    callbacks=[early_stopping],
)

Model: "sequential_2"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_10 (Dense)             (None, 512)               7168      
_________________________________________________________________
dropout (Dropout)            (None, 512)               0         
_________________________________________________________________
dense_11 (Dense)             (None, 1024)              525312    
_________________________________________________________________
dropout_1 (Dropout)          (None, 1024)              0         
_________________________________________________________________
dense_12 (Dense)             (None, 512)               524800    
_________________________________________________________________
dense_13 (Dense)             (None, 1)                 513       
=================================================================
Total params: 1,057,793
Trainable params: 1,057,793
Non-trainable params: 0
_________________________________________________________________
None
Epoch 1/1000
15/15 [==============================] - 1s 51ms/step - loss: 0.6459 - val_loss: 0.1513
Epoch 2/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.1613 - val_loss: 0.1027
Epoch 3/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.1056 - val_loss: 0.0918
Epoch 4/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0730 - val_loss: 0.0689
Epoch 5/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0566 - val_loss: 0.0742
Epoch 6/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0466 - val_loss: 0.0360
Epoch 7/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0409 - val_loss: 0.0673
Epoch 8/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0396 - val_loss: 0.0652
Epoch 9/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0339 - val_loss: 0.0702
Epoch 10/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0337 - val_loss: 0.0623
Epoch 11/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0329 - val_loss: 0.0561
Epoch 12/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0307 - val_loss: 0.0721
Epoch 13/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0294 - val_loss: 0.0828
Epoch 14/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0273 - val_loss: 0.0763
Epoch 15/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0267 - val_loss: 0.0672
Epoch 16/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0258 - val_loss: 0.0740
Epoch 17/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0249 - val_loss: 0.0462
Epoch 18/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0263 - val_loss: 0.0770
Epoch 19/1000
15/15 [==============================] - 1s 42ms/step - loss: 0.0246 - val_loss: 0.0679
Epoch 20/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0238 - val_loss: 0.0984
Epoch 21/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0246 - val_loss: 0.0536
Epoch 22/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0237 - val_loss: 0.0837
Epoch 23/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0214 - val_loss: 0.0754
Epoch 24/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0216 - val_loss: 0.0664
Epoch 25/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0222 - val_loss: 0.0631
Epoch 26/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0215 - val_loss: 0.0858

2.2.2 Batch Normalization

back to top

Batch normalization (batchnorm) accomplishes a task very similar to sklearn's StandardScaler, and in fact, it can be added to the front of a neural network in place of sklearn's StandardScaler to scale and center the input data. But batchnorm is also used between layers, why would we want to rescale the output from one layer before feeding into the next? For the same reason we would want to scale and center our data in the first place: it levels the playing field for the following layer to find the important relationships. The optimizer algorithm, SGD, will shift weights in proportion to how large the activation is out of each neuron, and so large differences can lead to spurious behavior.

In practice, batchnorm is often implemented to make the overall training time faster, rather than to improve the final loss (although in some cases it does do this as well). It is good to envoke batchnorm in particular, if you are dealing with neural networks that take a long time to train.

Batchnorm can be added between layers, as well as between a layer and its activation function.

# BatchNorm model

model = keras.Sequential([
    layers.Dense(512, activation='relu', input_shape=[X_train_std.shape[1]]),
    layers.BatchNormalization(),
    layers.Dense(512*2, activation='relu'),
    layers.BatchNormalization(),
    layers.Dense(512, activation='relu'),
    layers.Dense(1),
])

model.compile(
    optimizer='adam',
    loss='mse',
)

early_stopping = EarlyStopping(
    min_delta=0.001, # minimium amount of change to count as an improvement
    patience=20, # how many epochs to wait before stopping
    restore_best_weights=True,
)

print(model.summary())

history = model.fit(
    X_train_std, y_train_std,
    validation_data=(X_val_std, y_val_std),
    batch_size=256,
    epochs=1000,
    verbose=1,
    callbacks=[early_stopping],
)

Model: "sequential_3"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_14 (Dense)             (None, 512)               7168      
_________________________________________________________________
batch_normalization (BatchNo (None, 512)               2048      
_________________________________________________________________
dense_15 (Dense)             (None, 1024)              525312    
_________________________________________________________________
batch_normalization_1 (Batch (None, 1024)              4096      
_________________________________________________________________
dense_16 (Dense)             (None, 512)               524800    
_________________________________________________________________
dense_17 (Dense)             (None, 1)                 513       
=================================================================
Total params: 1,063,937
Trainable params: 1,060,865
Non-trainable params: 3,072
_________________________________________________________________
None
Epoch 1/1000
15/15 [==============================] - 2s 54ms/step - loss: 2.7890 - val_loss: 2.5754
Epoch 2/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.7404 - val_loss: 2.2122
Epoch 3/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.2845 - val_loss: 1.5998
Epoch 4/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.1671 - val_loss: 1.4054
Epoch 5/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.1195 - val_loss: 1.0034
Epoch 6/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.1000 - val_loss: 0.9543
Epoch 7/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.1353 - val_loss: 0.6496
Epoch 8/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.1688 - val_loss: 0.4768
Epoch 9/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.1562 - val_loss: 0.3414
Epoch 10/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.1296 - val_loss: 0.3393
Epoch 11/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0750 - val_loss: 0.2155
Epoch 12/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0512 - val_loss: 0.1708
Epoch 13/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0332 - val_loss: 0.1139
Epoch 14/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0329 - val_loss: 0.0851
Epoch 15/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0411 - val_loss: 0.0597
Epoch 16/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0455 - val_loss: 0.0591
Epoch 17/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0510 - val_loss: 0.0424
Epoch 18/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0381 - val_loss: 0.0549
Epoch 19/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0403 - val_loss: 0.0466
Epoch 20/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0290 - val_loss: 0.0468
Epoch 21/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0379 - val_loss: 0.0504
Epoch 22/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0444 - val_loss: 0.0553
Epoch 23/1000
15/15 [==============================] - 1s 43ms/step - loss: 0.0479 - val_loss: 0.0480
Epoch 24/1000
15/15 [==============================] - 1s 46ms/step - loss: 0.0331 - val_loss: 0.0400
Epoch 25/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0416 - val_loss: 0.0333
Epoch 26/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0396 - val_loss: 0.0276
Epoch 27/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0426 - val_loss: 0.0386
Epoch 28/1000
15/15 [==============================] - 1s 46ms/step - loss: 0.0308 - val_loss: 0.0427
Epoch 29/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0365 - val_loss: 0.0369
Epoch 30/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0337 - val_loss: 0.0393
Epoch 31/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0383 - val_loss: 0.0314
Epoch 32/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0358 - val_loss: 0.0533
Epoch 33/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0354 - val_loss: 0.0336
Epoch 34/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0332 - val_loss: 0.0363
Epoch 35/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0326 - val_loss: 0.0638
Epoch 36/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0459 - val_loss: 0.0427
Epoch 37/1000
15/15 [==============================] - 1s 46ms/step - loss: 0.0382 - val_loss: 0.0293
Epoch 38/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0440 - val_loss: 0.0446
Epoch 39/1000
15/15 [==============================] - 1s 47ms/step - loss: 0.0436 - val_loss: 0.0673
Epoch 40/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0535 - val_loss: 0.0354
Epoch 41/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0245 - val_loss: 0.0373
Epoch 42/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0225 - val_loss: 0.0313
Epoch 43/1000
15/15 [==============================] - 1s 47ms/step - loss: 0.0179 - val_loss: 0.0267
Epoch 44/1000
15/15 [==============================] - 1s 46ms/step - loss: 0.0174 - val_loss: 0.0427
Epoch 45/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0211 - val_loss: 0.0240
Epoch 46/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0139 - val_loss: 0.0275
Epoch 47/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0138 - val_loss: 0.0319
Epoch 48/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0205 - val_loss: 0.0237
Epoch 49/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0163 - val_loss: 0.0310
Epoch 50/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0169 - val_loss: 0.0259
Epoch 51/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0210 - val_loss: 0.0527
Epoch 52/1000
15/15 [==============================] - 1s 46ms/step - loss: 0.0261 - val_loss: 0.0432
Epoch 53/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0255 - val_loss: 0.0282
Epoch 54/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0246 - val_loss: 0.0268
Epoch 55/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0183 - val_loss: 0.0577
Epoch 56/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0236 - val_loss: 0.0276
Epoch 57/1000
15/15 [==============================] - 1s 46ms/step - loss: 0.0235 - val_loss: 0.0524
Epoch 58/1000
15/15 [==============================] - 1s 46ms/step - loss: 0.0308 - val_loss: 0.0517
Epoch 59/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0243 - val_loss: 0.0433
Epoch 60/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0207 - val_loss: 0.0293
Epoch 61/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0191 - val_loss: 0.0307
Epoch 62/1000
15/15 [==============================] - 1s 44ms/step - loss: 0.0183 - val_loss: 0.0350
Epoch 63/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0252 - val_loss: 0.0460
Epoch 64/1000
15/15 [==============================] - 1s 45ms/step - loss: 0.0281 - val_loss: 0.0365
Epoch 65/1000
15/15 [==============================] - 1s 46ms/step - loss: 0.0459 - val_loss: 0.0656

# Show the learning curves
history_df = pd.DataFrame(history.history)
fig, ax = plt.subplots(1,1)
history_df.plot(ax=ax)
ax.set_ylim(0,.2)

(0.0, 0.2)

y_test_pred = np.exp(model.predict(X_test_std))
plt.plot(y_test_pred, np.exp(y_test_std), ls='', marker='o')

[<matplotlib.lines.Line2D at 0x7f4c3ceb5150>]

Model with BatchNorm and Dropout:

from tensorflow import keras
from tensorflow.keras import layers

# Dropout and BatchNorm Model
model = keras.Sequential([
    layers.Dense(512, input_shape=[X_train_std.shape[1]]),
    layers.BatchNormalization(),
    layers.Activation('relu'), # separate activation
    layers.Dropout(0.3),
    layers.Dense(1024, activation='relu'), # built-in activation
    layers.Dropout(0.3),
    layers.BatchNormalization(),
    layers.Dense(512, activation='relu'),
    layers.Dropout(0.3),
    layers.BatchNormalization(),
    layers.Dense(1),
])

print(model.summary())

Model: "sequential_4"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_18 (Dense)             (None, 512)               7168      
_________________________________________________________________
batch_normalization_2 (Batch (None, 512)               2048      
_________________________________________________________________
activation (Activation)      (None, 512)               0         
_________________________________________________________________
dropout_2 (Dropout)          (None, 512)               0         
_________________________________________________________________
dense_19 (Dense)             (None, 1024)              525312    
_________________________________________________________________
dropout_3 (Dropout)          (None, 1024)              0         
_________________________________________________________________
batch_normalization_3 (Batch (None, 1024)              4096      
_________________________________________________________________
dense_20 (Dense)             (None, 512)               524800    
_________________________________________________________________
dropout_4 (Dropout)          (None, 512)               0         
_________________________________________________________________
batch_normalization_4 (Batch (None, 512)               2048      
_________________________________________________________________
dense_21 (Dense)             (None, 1)                 513       
=================================================================
Total params: 1,065,985
Trainable params: 1,061,889
Non-trainable params: 4,096
_________________________________________________________________
None

🏋️ Exercise 2: Try Batch Normalization and Dropout

Create 3 models and train for 100 epochs with early stopping:

1. compile and train the model previously defined above
2. recreate the architecture but remove the batchnorm layers
3. recreate the architecture but remove the dropout layers and one hidden, dense layer

Compare the number of epochs required to converge, and the overall loss

# Dropout and BatchNorm Model
model = keras.Sequential([                      
    ### YOUR CODE HERE ###

])

model.compile(
    optimizer='adam',
    loss='mae',
)

early_stopping = EarlyStopping(
    min_delta=0.001, # minimium amount of change to count as an improvement
    patience=20, # how many epochs to wait before stopping
    restore_best_weights=True,
)

history = model.fit(
    X_train_std, y_train_std,
    validation_data=(X_val_std, y_val_std),
    batch_size=256,
    epochs=100,
    verbose=1,
    callbacks=[early_stopping],
)

Epoch 1/100
15/15 [==============================] - 1s 16ms/step - loss: 1.7653 - val_loss: 1.3092
Epoch 2/100
15/15 [==============================] - 0s 6ms/step - loss: 1.3614 - val_loss: 0.9521
Epoch 3/100
15/15 [==============================] - 0s 7ms/step - loss: 1.0655 - val_loss: 0.6253
Epoch 4/100
15/15 [==============================] - 0s 7ms/step - loss: 0.8148 - val_loss: 0.3236
Epoch 5/100
15/15 [==============================] - 0s 6ms/step - loss: 0.6566 - val_loss: 0.2231
Epoch 6/100
15/15 [==============================] - 0s 6ms/step - loss: 0.5569 - val_loss: 0.1752
Epoch 7/100
15/15 [==============================] - 0s 6ms/step - loss: 0.5185 - val_loss: 0.1731
Epoch 8/100
15/15 [==============================] - 0s 6ms/step - loss: 0.4466 - val_loss: 0.1596
Epoch 9/100
15/15 [==============================] - 0s 6ms/step - loss: 0.4092 - val_loss: 0.1712
Epoch 10/100
15/15 [==============================] - 0s 7ms/step - loss: 0.3836 - val_loss: 0.1516
Epoch 11/100
15/15 [==============================] - 0s 7ms/step - loss: 0.3530 - val_loss: 0.1603
Epoch 12/100
15/15 [==============================] - 0s 6ms/step - loss: 0.3323 - val_loss: 0.1423
Epoch 13/100
15/15 [==============================] - 0s 6ms/step - loss: 0.3423 - val_loss: 0.1385
Epoch 14/100
15/15 [==============================] - 0s 7ms/step - loss: 0.3116 - val_loss: 0.1289
Epoch 15/100
15/15 [==============================] - 0s 7ms/step - loss: 0.3055 - val_loss: 0.1269
Epoch 16/100
15/15 [==============================] - 0s 7ms/step - loss: 0.2849 - val_loss: 0.1067
Epoch 17/100
15/15 [==============================] - 0s 6ms/step - loss: 0.2813 - val_loss: 0.1116
Epoch 18/100
15/15 [==============================] - 0s 6ms/step - loss: 0.2737 - val_loss: 0.1163
Epoch 19/100
15/15 [==============================] - 0s 6ms/step - loss: 0.2520 - val_loss: 0.1149
Epoch 20/100
15/15 [==============================] - 0s 6ms/step - loss: 0.2454 - val_loss: 0.1366
Epoch 21/100
15/15 [==============================] - 0s 6ms/step - loss: 0.2406 - val_loss: 0.1094
Epoch 22/100
15/15 [==============================] - 0s 6ms/step - loss: 0.2334 - val_loss: 0.1069
Epoch 23/100
15/15 [==============================] - 0s 6ms/step - loss: 0.2283 - val_loss: 0.1109
Epoch 24/100
15/15 [==============================] - 0s 6ms/step - loss: 0.2116 - val_loss: 0.1092
Epoch 25/100
15/15 [==============================] - 0s 6ms/step - loss: 0.2048 - val_loss: 0.1024
Epoch 26/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1885 - val_loss: 0.1004
Epoch 27/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1979 - val_loss: 0.1115
Epoch 28/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1863 - val_loss: 0.1077
Epoch 29/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1713 - val_loss: 0.1106
Epoch 30/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1756 - val_loss: 0.1057
Epoch 31/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1598 - val_loss: 0.1120
Epoch 32/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1706 - val_loss: 0.1153
Epoch 33/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1553 - val_loss: 0.1175
Epoch 34/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1628 - val_loss: 0.1051
Epoch 35/100
15/15 [==============================] - 0s 7ms/step - loss: 0.1538 - val_loss: 0.0985
Epoch 36/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1472 - val_loss: 0.1005
Epoch 37/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1447 - val_loss: 0.0950
Epoch 38/100
15/15 [==============================] - 0s 7ms/step - loss: 0.1439 - val_loss: 0.1088
Epoch 39/100
15/15 [==============================] - 0s 7ms/step - loss: 0.1530 - val_loss: 0.1176
Epoch 40/100
15/15 [==============================] - 0s 7ms/step - loss: 0.1400 - val_loss: 0.1240
Epoch 41/100
15/15 [==============================] - 0s 7ms/step - loss: 0.1438 - val_loss: 0.0981
Epoch 42/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1410 - val_loss: 0.0963
Epoch 43/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1420 - val_loss: 0.0972
Epoch 44/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1468 - val_loss: 0.1168
Epoch 45/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1419 - val_loss: 0.0949
Epoch 46/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1401 - val_loss: 0.0940
Epoch 47/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1394 - val_loss: 0.0970
Epoch 48/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1368 - val_loss: 0.1291
Epoch 49/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1445 - val_loss: 0.1008
Epoch 50/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1467 - val_loss: 0.1030
Epoch 51/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1404 - val_loss: 0.1066
Epoch 52/100
15/15 [==============================] - 0s 7ms/step - loss: 0.1420 - val_loss: 0.0946
Epoch 53/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1370 - val_loss: 0.0946
Epoch 54/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1367 - val_loss: 0.1009
Epoch 55/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1403 - val_loss: 0.1037
Epoch 56/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1377 - val_loss: 0.1040
Epoch 57/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1377 - val_loss: 0.0935
Epoch 58/100
15/15 [==============================] - 0s 7ms/step - loss: 0.1420 - val_loss: 0.0921
Epoch 59/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1333 - val_loss: 0.0990
Epoch 60/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1305 - val_loss: 0.1067
Epoch 61/100
15/15 [==============================] - 0s 7ms/step - loss: 0.1362 - val_loss: 0.1123
Epoch 62/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1344 - val_loss: 0.0942
Epoch 63/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1267 - val_loss: 0.0981
Epoch 64/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1247 - val_loss: 0.0904
Epoch 65/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1307 - val_loss: 0.0979
Epoch 66/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1321 - val_loss: 0.0976
Epoch 67/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1325 - val_loss: 0.1214
Epoch 68/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1340 - val_loss: 0.1112
Epoch 69/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1290 - val_loss: 0.1022
Epoch 70/100
15/15 [==============================] - 0s 7ms/step - loss: 0.1330 - val_loss: 0.1014
Epoch 71/100
15/15 [==============================] - 0s 8ms/step - loss: 0.1274 - val_loss: 0.0989
Epoch 72/100
15/15 [==============================] - 0s 8ms/step - loss: 0.1179 - val_loss: 0.0913
Epoch 73/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1157 - val_loss: 0.0970
Epoch 74/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1280 - val_loss: 0.0909
Epoch 75/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1203 - val_loss: 0.0940
Epoch 76/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1293 - val_loss: 0.0934
Epoch 77/100
15/15 [==============================] - 0s 7ms/step - loss: 0.1300 - val_loss: 0.0975
Epoch 78/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1257 - val_loss: 0.0915
Epoch 79/100
15/15 [==============================] - 0s 7ms/step - loss: 0.1265 - val_loss: 0.0975
Epoch 80/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1192 - val_loss: 0.0906
Epoch 81/100
15/15 [==============================] - 0s 7ms/step - loss: 0.1214 - val_loss: 0.0902
Epoch 82/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1209 - val_loss: 0.0994
Epoch 83/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1200 - val_loss: 0.0971
Epoch 84/100
15/15 [==============================] - 0s 6ms/step - loss: 0.1238 - val_loss: 0.0942

2.3 Binary Classification with Neural Networks

When dealing with classification tasks, everything we've covered up till now with regression still applies. The main difference is the format of the last layer's outputs and the choice of loss function.

2.3.1 Accuracy and Cross Entropy

Formerly, we've encountered accuracy in classification tasks. It is the ratio of correct predictions over total predictions: accuracy = number_corect / total (and when classes were heavily imballanced we used a weighted accuracy).

The problem with using accuracy as a loss function, is that it does not change smoothly (there are jumps in the numerator since it is just a count in correct predictions), which the SGD algorithm requires in order to work properly. We need another metric.

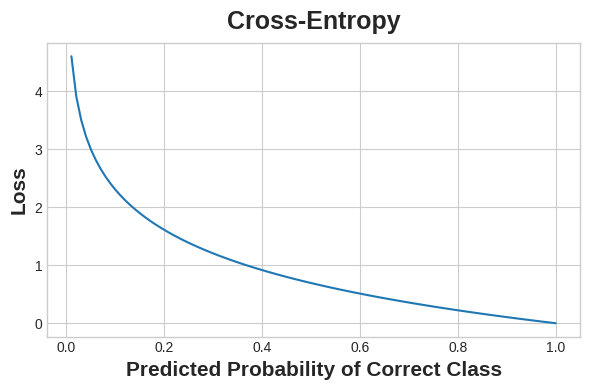
the further a model is from predicting the correct class, the higher the loss.

Instead we use cross-entropy, we won't go into detail here, other than that it is a distance measure between two probabilities (the probability of predicting the class or the incorrect class). We want the probability for predicting the correct class to be 1 (100%) and cross-entropy will measure the distance the current probability of the model is from 1.

We set cross-entropy as our loss when we compile the model. In this case we have two classes so we use binary_crossentropy

model.compile(
    # optimizer...
    loss='binary_crossentropy',
    metrics=['binary_accuracy'],
)

2.3.2 0 or 1: The Sigmoid Function

Finally, we need to introduce a special activation function that will map our last layer outputs from 0 to 1, to feed into our loss function. The traditional function we use for this is the sigmoid function.

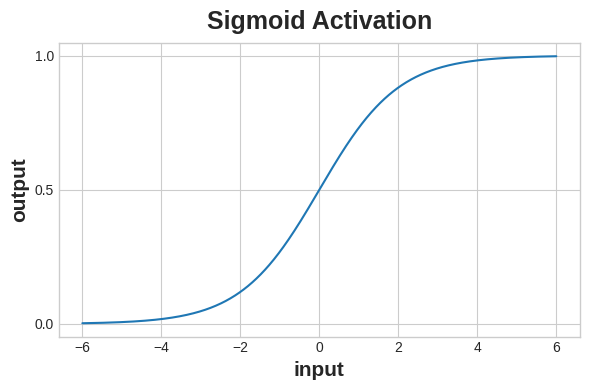
The sigmoid function maps values on the interval [0, 1]

To get the final class prediction, we need a threshold probability, typically 0.5 where we will round up to the class label. Keras will set to 0.5 by default.

We set the sigmoid activation function in the last layer:

model = keras.Sequential([
    # ... previous layers ...
    layers.Dense(1, activation='sigmoid'),
])

2.3.3 Classification Example

wine = pd.read_csv("https://raw.githubusercontent.com/wesleybeckner/"\
      "ds_for_engineers/main/data/wine_quality/winequalityN.csv")

# create X and y
X = wine.copy()
y = X.pop('type')

# split into train/test
X_train, X_test, y_train, y_test = train_test_split(X, y)
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train)

# the numerical values pipe
num_proc = make_pipeline(SimpleImputer(strategy='median'), StandardScaler())

# the categorical values pipe
cat_proc = make_pipeline(
    SimpleImputer(strategy='constant', fill_value='missing'),
    OneHotEncoder(handle_unknown='ignore'))

# parallelize the two pipes
preprocessor = make_column_transformer((num_proc,
                                make_column_selector(dtype_include=np.number)),
                                       (cat_proc,
                                make_column_selector(dtype_include=object)))

X_train_std = preprocessor.fit_transform(X_train) # fit_transform on train
X_test_std = preprocessor.transform(X_test) # transform test
X_val_std = preprocessor.transform(X_val)

y_train_std = y_train.map({'white': 0, 'red': 1}) # convert to int
y_val_std = y_val.map({'white': 0, 'red': 1}) # convert to int
y_test_std = y_test.map({'white': 0, 'red': 1}) # convert to int

preprocessor

ColumnTransformer

ColumnTransformer(transformers=[('pipeline-1',
                                 Pipeline(steps=[('simpleimputer',
                                                  SimpleImputer(strategy='median')),
                                                 ('standardscaler',
                                                  StandardScaler())]),
                                 ),
                                ('pipeline-2',
                                 Pipeline(steps=[('simpleimputer',
                                                  SimpleImputer(fill_value='missing',
                                                                strategy='constant')),
                                                 ('onehotencoder',
                                                  OneHotEncoder(handle_unknown='ignore'))]),
                                 )])

pipeline-1

SimpleImputer

SimpleImputer(strategy='median')

StandardScaler

StandardScaler()

pipeline-2

SimpleImputer

SimpleImputer(fill_value='missing', strategy='constant')

OneHotEncoder

OneHotEncoder(handle_unknown='ignore')

from tensorflow import keras
from tensorflow.keras import layers

model = keras.Sequential([
    layers.Dense(4, activation='relu', input_shape=[X_train_std.shape[1]]),
    layers.Dense(4, activation='relu'),    
    layers.Dense(1, activation='sigmoid'),
])

print(model.summary())

Model: "sequential_5"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_22 (Dense)             (None, 4)                 52        
_________________________________________________________________
dense_23 (Dense)             (None, 4)                 20        
_________________________________________________________________
dense_24 (Dense)             (None, 1)                 5         
=================================================================
Total params: 77
Trainable params: 77
Non-trainable params: 0
_________________________________________________________________
None

tf.keras.utils.plot_model(model, 
                          show_layer_names=True, 
                          # show_dtype=True, 
                          show_shapes=True)

We set cross-entropy as our loss when we compile the model. In this case we have two classes so we use binary_crossentropy

Introducing metrics: we can track other forms of performance during training with the metrics parameter in model.compile. We will look at the results when we finish training.

model.compile(
    optimizer='adam',
    loss='binary_crossentropy',
    metrics=['binary_accuracy'], # new metrics flag here
)

early_stopping = keras.callbacks.EarlyStopping(
    patience=10,
    min_delta=0.001,
    restore_best_weights=True,
)

history = model.fit(
    X_train_std, y_train_std,
    validation_data=(X_val_std, y_val_std),
    batch_size=512,
    epochs=1000,
    callbacks=[early_stopping],
    verbose=1, 
)

Epoch 1/1000
8/8 [==============================] - 1s 21ms/step - loss: 0.6466 - binary_accuracy: 0.6292 - val_loss: 0.6328 - val_binary_accuracy: 0.6371
Epoch 2/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.6336 - binary_accuracy: 0.6623 - val_loss: 0.6196 - val_binary_accuracy: 0.6658
Epoch 3/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.6207 - binary_accuracy: 0.6891 - val_loss: 0.6066 - val_binary_accuracy: 0.6954
Epoch 4/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.6079 - binary_accuracy: 0.7154 - val_loss: 0.5938 - val_binary_accuracy: 0.7192
Epoch 5/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.5951 - binary_accuracy: 0.7365 - val_loss: 0.5812 - val_binary_accuracy: 0.7381
Epoch 6/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.5826 - binary_accuracy: 0.7597 - val_loss: 0.5687 - val_binary_accuracy: 0.7594
Epoch 7/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.5700 - binary_accuracy: 0.7756 - val_loss: 0.5559 - val_binary_accuracy: 0.7750
Epoch 8/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.5573 - binary_accuracy: 0.7909 - val_loss: 0.5428 - val_binary_accuracy: 0.7939
Epoch 9/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.5444 - binary_accuracy: 0.8041 - val_loss: 0.5295 - val_binary_accuracy: 0.8095
Epoch 10/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.5315 - binary_accuracy: 0.8158 - val_loss: 0.5162 - val_binary_accuracy: 0.8194
Epoch 11/1000
8/8 [==============================] - 0s 8ms/step - loss: 0.5184 - binary_accuracy: 0.8281 - val_loss: 0.5028 - val_binary_accuracy: 0.8300
Epoch 12/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.5051 - binary_accuracy: 0.8388 - val_loss: 0.4890 - val_binary_accuracy: 0.8415
Epoch 13/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.4913 - binary_accuracy: 0.8498 - val_loss: 0.4748 - val_binary_accuracy: 0.8539
Epoch 14/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.4771 - binary_accuracy: 0.8580 - val_loss: 0.4601 - val_binary_accuracy: 0.8629
Epoch 15/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.4627 - binary_accuracy: 0.8675 - val_loss: 0.4454 - val_binary_accuracy: 0.8695
Epoch 16/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.4478 - binary_accuracy: 0.8725 - val_loss: 0.4309 - val_binary_accuracy: 0.8727
Epoch 17/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.4327 - binary_accuracy: 0.8788 - val_loss: 0.4163 - val_binary_accuracy: 0.8785
Epoch 18/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.4172 - binary_accuracy: 0.8831 - val_loss: 0.4014 - val_binary_accuracy: 0.8826
Epoch 19/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.4015 - binary_accuracy: 0.8886 - val_loss: 0.3863 - val_binary_accuracy: 0.8892
Epoch 20/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.3857 - binary_accuracy: 0.8944 - val_loss: 0.3710 - val_binary_accuracy: 0.8957
Epoch 21/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.3695 - binary_accuracy: 0.9015 - val_loss: 0.3554 - val_binary_accuracy: 0.9064
Epoch 22/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.3536 - binary_accuracy: 0.9078 - val_loss: 0.3400 - val_binary_accuracy: 0.9130
Epoch 23/1000
8/8 [==============================] - 0s 4ms/step - loss: 0.3380 - binary_accuracy: 0.9168 - val_loss: 0.3247 - val_binary_accuracy: 0.9195
Epoch 24/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.3226 - binary_accuracy: 0.9228 - val_loss: 0.3098 - val_binary_accuracy: 0.9286
Epoch 25/1000
8/8 [==============================] - 0s 4ms/step - loss: 0.3074 - binary_accuracy: 0.9297 - val_loss: 0.2953 - val_binary_accuracy: 0.9392
Epoch 26/1000
8/8 [==============================] - 0s 7ms/step - loss: 0.2926 - binary_accuracy: 0.9360 - val_loss: 0.2811 - val_binary_accuracy: 0.9417
Epoch 27/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.2780 - binary_accuracy: 0.9409 - val_loss: 0.2671 - val_binary_accuracy: 0.9499
Epoch 28/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.2639 - binary_accuracy: 0.9480 - val_loss: 0.2537 - val_binary_accuracy: 0.9548
Epoch 29/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.2502 - binary_accuracy: 0.9540 - val_loss: 0.2408 - val_binary_accuracy: 0.9581
Epoch 30/1000
8/8 [==============================] - 0s 4ms/step - loss: 0.2373 - binary_accuracy: 0.9589 - val_loss: 0.2285 - val_binary_accuracy: 0.9606
Epoch 31/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.2248 - binary_accuracy: 0.9625 - val_loss: 0.2168 - val_binary_accuracy: 0.9663
Epoch 32/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.2129 - binary_accuracy: 0.9658 - val_loss: 0.2056 - val_binary_accuracy: 0.9672
Epoch 33/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.2017 - binary_accuracy: 0.9699 - val_loss: 0.1948 - val_binary_accuracy: 0.9688
Epoch 34/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.1910 - binary_accuracy: 0.9729 - val_loss: 0.1849 - val_binary_accuracy: 0.9713
Epoch 35/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.1811 - binary_accuracy: 0.9762 - val_loss: 0.1755 - val_binary_accuracy: 0.9745
Epoch 36/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.1718 - binary_accuracy: 0.9787 - val_loss: 0.1665 - val_binary_accuracy: 0.9770
Epoch 37/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.1630 - binary_accuracy: 0.9795 - val_loss: 0.1582 - val_binary_accuracy: 0.9778
Epoch 38/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.1546 - binary_accuracy: 0.9806 - val_loss: 0.1504 - val_binary_accuracy: 0.9778
Epoch 39/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.1468 - binary_accuracy: 0.9806 - val_loss: 0.1431 - val_binary_accuracy: 0.9778
Epoch 40/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.1394 - binary_accuracy: 0.9817 - val_loss: 0.1362 - val_binary_accuracy: 0.9803
Epoch 41/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.1326 - binary_accuracy: 0.9819 - val_loss: 0.1297 - val_binary_accuracy: 0.9819
Epoch 42/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.1262 - binary_accuracy: 0.9839 - val_loss: 0.1237 - val_binary_accuracy: 0.9819
Epoch 43/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.1202 - binary_accuracy: 0.9849 - val_loss: 0.1183 - val_binary_accuracy: 0.9828
Epoch 44/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.1147 - binary_accuracy: 0.9849 - val_loss: 0.1132 - val_binary_accuracy: 0.9828
Epoch 45/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.1096 - binary_accuracy: 0.9852 - val_loss: 0.1085 - val_binary_accuracy: 0.9844
Epoch 46/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.1048 - binary_accuracy: 0.9858 - val_loss: 0.1042 - val_binary_accuracy: 0.9844
Epoch 47/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.1003 - binary_accuracy: 0.9866 - val_loss: 0.1001 - val_binary_accuracy: 0.9852
Epoch 48/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0962 - binary_accuracy: 0.9866 - val_loss: 0.0963 - val_binary_accuracy: 0.9860
Epoch 49/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0923 - binary_accuracy: 0.9869 - val_loss: 0.0929 - val_binary_accuracy: 0.9869
Epoch 50/1000
8/8 [==============================] - 0s 4ms/step - loss: 0.0889 - binary_accuracy: 0.9869 - val_loss: 0.0898 - val_binary_accuracy: 0.9877
Epoch 51/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0856 - binary_accuracy: 0.9871 - val_loss: 0.0868 - val_binary_accuracy: 0.9877
Epoch 52/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0826 - binary_accuracy: 0.9874 - val_loss: 0.0840 - val_binary_accuracy: 0.9877
Epoch 53/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0798 - binary_accuracy: 0.9871 - val_loss: 0.0813 - val_binary_accuracy: 0.9877
Epoch 54/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0771 - binary_accuracy: 0.9877 - val_loss: 0.0788 - val_binary_accuracy: 0.9877
Epoch 55/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0747 - binary_accuracy: 0.9880 - val_loss: 0.0765 - val_binary_accuracy: 0.9877
Epoch 56/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0725 - binary_accuracy: 0.9885 - val_loss: 0.0744 - val_binary_accuracy: 0.9877
Epoch 57/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0704 - binary_accuracy: 0.9882 - val_loss: 0.0726 - val_binary_accuracy: 0.9877
Epoch 58/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0685 - binary_accuracy: 0.9882 - val_loss: 0.0708 - val_binary_accuracy: 0.9877
Epoch 59/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0667 - binary_accuracy: 0.9880 - val_loss: 0.0691 - val_binary_accuracy: 0.9869
Epoch 60/1000
8/8 [==============================] - 0s 8ms/step - loss: 0.0651 - binary_accuracy: 0.9882 - val_loss: 0.0675 - val_binary_accuracy: 0.9869
Epoch 61/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0635 - binary_accuracy: 0.9888 - val_loss: 0.0661 - val_binary_accuracy: 0.9869
Epoch 62/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0620 - binary_accuracy: 0.9888 - val_loss: 0.0647 - val_binary_accuracy: 0.9869
Epoch 63/1000
8/8 [==============================] - 0s 8ms/step - loss: 0.0607 - binary_accuracy: 0.9893 - val_loss: 0.0635 - val_binary_accuracy: 0.9869
Epoch 64/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0594 - binary_accuracy: 0.9896 - val_loss: 0.0623 - val_binary_accuracy: 0.9877
Epoch 65/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0582 - binary_accuracy: 0.9893 - val_loss: 0.0612 - val_binary_accuracy: 0.9877
Epoch 66/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0571 - binary_accuracy: 0.9896 - val_loss: 0.0601 - val_binary_accuracy: 0.9877
Epoch 67/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0559 - binary_accuracy: 0.9896 - val_loss: 0.0591 - val_binary_accuracy: 0.9877
Epoch 68/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0549 - binary_accuracy: 0.9896 - val_loss: 0.0581 - val_binary_accuracy: 0.9877
Epoch 69/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0539 - binary_accuracy: 0.9896 - val_loss: 0.0572 - val_binary_accuracy: 0.9877
Epoch 70/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0529 - binary_accuracy: 0.9896 - val_loss: 0.0563 - val_binary_accuracy: 0.9885
Epoch 71/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0521 - binary_accuracy: 0.9899 - val_loss: 0.0554 - val_binary_accuracy: 0.9885
Epoch 72/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0512 - binary_accuracy: 0.9901 - val_loss: 0.0546 - val_binary_accuracy: 0.9885
Epoch 73/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0505 - binary_accuracy: 0.9901 - val_loss: 0.0539 - val_binary_accuracy: 0.9885
Epoch 74/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0498 - binary_accuracy: 0.9901 - val_loss: 0.0532 - val_binary_accuracy: 0.9885
Epoch 75/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0492 - binary_accuracy: 0.9901 - val_loss: 0.0525 - val_binary_accuracy: 0.9885
Epoch 76/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0485 - binary_accuracy: 0.9901 - val_loss: 0.0519 - val_binary_accuracy: 0.9885
Epoch 77/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0479 - binary_accuracy: 0.9901 - val_loss: 0.0514 - val_binary_accuracy: 0.9885
Epoch 78/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0473 - binary_accuracy: 0.9901 - val_loss: 0.0509 - val_binary_accuracy: 0.9885
Epoch 79/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0468 - binary_accuracy: 0.9901 - val_loss: 0.0504 - val_binary_accuracy: 0.9885
Epoch 80/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0463 - binary_accuracy: 0.9901 - val_loss: 0.0499 - val_binary_accuracy: 0.9885
Epoch 81/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0458 - binary_accuracy: 0.9901 - val_loss: 0.0494 - val_binary_accuracy: 0.9893
Epoch 82/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0454 - binary_accuracy: 0.9901 - val_loss: 0.0490 - val_binary_accuracy: 0.9893
Epoch 83/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0450 - binary_accuracy: 0.9901 - val_loss: 0.0486 - val_binary_accuracy: 0.9901
Epoch 84/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0446 - binary_accuracy: 0.9901 - val_loss: 0.0481 - val_binary_accuracy: 0.9901
Epoch 85/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0442 - binary_accuracy: 0.9904 - val_loss: 0.0478 - val_binary_accuracy: 0.9901
Epoch 86/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0438 - binary_accuracy: 0.9904 - val_loss: 0.0475 - val_binary_accuracy: 0.9901
Epoch 87/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0434 - binary_accuracy: 0.9904 - val_loss: 0.0472 - val_binary_accuracy: 0.9901
Epoch 88/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0431 - binary_accuracy: 0.9904 - val_loss: 0.0469 - val_binary_accuracy: 0.9901
Epoch 89/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0428 - binary_accuracy: 0.9904 - val_loss: 0.0465 - val_binary_accuracy: 0.9910
Epoch 90/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0425 - binary_accuracy: 0.9904 - val_loss: 0.0463 - val_binary_accuracy: 0.9910
Epoch 91/1000
8/8 [==============================] - 0s 7ms/step - loss: 0.0422 - binary_accuracy: 0.9904 - val_loss: 0.0460 - val_binary_accuracy: 0.9910
Epoch 92/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0419 - binary_accuracy: 0.9907 - val_loss: 0.0457 - val_binary_accuracy: 0.9910
Epoch 93/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0416 - binary_accuracy: 0.9907 - val_loss: 0.0455 - val_binary_accuracy: 0.9910
Epoch 94/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0413 - binary_accuracy: 0.9907 - val_loss: 0.0452 - val_binary_accuracy: 0.9910
Epoch 95/1000
8/8 [==============================] - 0s 8ms/step - loss: 0.0410 - binary_accuracy: 0.9907 - val_loss: 0.0450 - val_binary_accuracy: 0.9910
Epoch 96/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0408 - binary_accuracy: 0.9907 - val_loss: 0.0448 - val_binary_accuracy: 0.9910
Epoch 97/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0405 - binary_accuracy: 0.9907 - val_loss: 0.0446 - val_binary_accuracy: 0.9910
Epoch 98/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0403 - binary_accuracy: 0.9907 - val_loss: 0.0444 - val_binary_accuracy: 0.9910
Epoch 99/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0400 - binary_accuracy: 0.9912 - val_loss: 0.0442 - val_binary_accuracy: 0.9910
Epoch 100/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0398 - binary_accuracy: 0.9915 - val_loss: 0.0439 - val_binary_accuracy: 0.9910
Epoch 101/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0396 - binary_accuracy: 0.9915 - val_loss: 0.0437 - val_binary_accuracy: 0.9910
Epoch 102/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0394 - binary_accuracy: 0.9915 - val_loss: 0.0436 - val_binary_accuracy: 0.9910
Epoch 103/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0391 - binary_accuracy: 0.9915 - val_loss: 0.0434 - val_binary_accuracy: 0.9910
Epoch 104/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0390 - binary_accuracy: 0.9915 - val_loss: 0.0432 - val_binary_accuracy: 0.9910
Epoch 105/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0388 - binary_accuracy: 0.9915 - val_loss: 0.0430 - val_binary_accuracy: 0.9910
Epoch 106/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0385 - binary_accuracy: 0.9918 - val_loss: 0.0428 - val_binary_accuracy: 0.9910
Epoch 107/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0383 - binary_accuracy: 0.9918 - val_loss: 0.0427 - val_binary_accuracy: 0.9918
Epoch 108/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0381 - binary_accuracy: 0.9918 - val_loss: 0.0425 - val_binary_accuracy: 0.9918
Epoch 109/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0380 - binary_accuracy: 0.9918 - val_loss: 0.0423 - val_binary_accuracy: 0.9918
Epoch 110/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0378 - binary_accuracy: 0.9921 - val_loss: 0.0421 - val_binary_accuracy: 0.9918
Epoch 111/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0376 - binary_accuracy: 0.9921 - val_loss: 0.0420 - val_binary_accuracy: 0.9918
Epoch 112/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0374 - binary_accuracy: 0.9921 - val_loss: 0.0419 - val_binary_accuracy: 0.9918
Epoch 113/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0372 - binary_accuracy: 0.9918 - val_loss: 0.0417 - val_binary_accuracy: 0.9918
Epoch 114/1000
8/8 [==============================] - 0s 7ms/step - loss: 0.0371 - binary_accuracy: 0.9918 - val_loss: 0.0415 - val_binary_accuracy: 0.9918
Epoch 115/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0369 - binary_accuracy: 0.9921 - val_loss: 0.0414 - val_binary_accuracy: 0.9918
Epoch 116/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0368 - binary_accuracy: 0.9921 - val_loss: 0.0413 - val_binary_accuracy: 0.9918
Epoch 117/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0366 - binary_accuracy: 0.9921 - val_loss: 0.0411 - val_binary_accuracy: 0.9926
Epoch 118/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0365 - binary_accuracy: 0.9921 - val_loss: 0.0410 - val_binary_accuracy: 0.9918
Epoch 119/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0364 - binary_accuracy: 0.9923 - val_loss: 0.0409 - val_binary_accuracy: 0.9918
Epoch 120/1000
8/8 [==============================] - 0s 7ms/step - loss: 0.0363 - binary_accuracy: 0.9923 - val_loss: 0.0408 - val_binary_accuracy: 0.9918
Epoch 121/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0361 - binary_accuracy: 0.9923 - val_loss: 0.0406 - val_binary_accuracy: 0.9918
Epoch 122/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0360 - binary_accuracy: 0.9923 - val_loss: 0.0405 - val_binary_accuracy: 0.9918
Epoch 123/1000
8/8 [==============================] - 0s 8ms/step - loss: 0.0359 - binary_accuracy: 0.9923 - val_loss: 0.0403 - val_binary_accuracy: 0.9918
Epoch 124/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0357 - binary_accuracy: 0.9923 - val_loss: 0.0402 - val_binary_accuracy: 0.9918
Epoch 125/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0356 - binary_accuracy: 0.9923 - val_loss: 0.0401 - val_binary_accuracy: 0.9918
Epoch 126/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0355 - binary_accuracy: 0.9923 - val_loss: 0.0399 - val_binary_accuracy: 0.9926
Epoch 127/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0354 - binary_accuracy: 0.9926 - val_loss: 0.0398 - val_binary_accuracy: 0.9926
Epoch 128/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0353 - binary_accuracy: 0.9926 - val_loss: 0.0397 - val_binary_accuracy: 0.9926
Epoch 129/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0352 - binary_accuracy: 0.9926 - val_loss: 0.0395 - val_binary_accuracy: 0.9926
Epoch 130/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0351 - binary_accuracy: 0.9926 - val_loss: 0.0394 - val_binary_accuracy: 0.9926
Epoch 131/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0350 - binary_accuracy: 0.9926 - val_loss: 0.0393 - val_binary_accuracy: 0.9918
Epoch 132/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0349 - binary_accuracy: 0.9926 - val_loss: 0.0392 - val_binary_accuracy: 0.9918
Epoch 133/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0348 - binary_accuracy: 0.9926 - val_loss: 0.0392 - val_binary_accuracy: 0.9918
Epoch 134/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0347 - binary_accuracy: 0.9929 - val_loss: 0.0391 - val_binary_accuracy: 0.9918
Epoch 135/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0345 - binary_accuracy: 0.9926 - val_loss: 0.0390 - val_binary_accuracy: 0.9918
Epoch 136/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0344 - binary_accuracy: 0.9929 - val_loss: 0.0389 - val_binary_accuracy: 0.9918
Epoch 137/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0344 - binary_accuracy: 0.9929 - val_loss: 0.0388 - val_binary_accuracy: 0.9918
Epoch 138/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0343 - binary_accuracy: 0.9932 - val_loss: 0.0387 - val_binary_accuracy: 0.9926
Epoch 139/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0342 - binary_accuracy: 0.9932 - val_loss: 0.0386 - val_binary_accuracy: 0.9918
Epoch 140/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0341 - binary_accuracy: 0.9932 - val_loss: 0.0385 - val_binary_accuracy: 0.9918
Epoch 141/1000
8/8 [==============================] - 0s 6ms/step - loss: 0.0339 - binary_accuracy: 0.9929 - val_loss: 0.0384 - val_binary_accuracy: 0.9918
Epoch 142/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0338 - binary_accuracy: 0.9929 - val_loss: 0.0383 - val_binary_accuracy: 0.9918
Epoch 143/1000
8/8 [==============================] - 0s 5ms/step - loss: 0.0337 - binary_accuracy: 0.9929 - val_loss: 0.0382 - val_binary_accuracy: 0.9918
Epoch 144/1000
8/8 [==============================] - 0s 7ms/step - loss: 0.0336 - binary_accuracy: 0.9929 - val_loss: 0.0382 - val_binary_accuracy: 0.9918

history_df = pd.DataFrame(history.history)

history_df.loc[:, ['loss', 'val_loss']].plot()
history_df.loc[:, ['binary_accuracy', 'val_binary_accuracy']].plot()

print(("Best Validation Loss: {:0.4f}" +\
      "\nBest Validation Accuracy: {:0.4f}")\
      .format(history_df['val_loss'].min(), 
              history_df['val_binary_accuracy'].max()))

Best Validation Loss: 0.0382
Best Validation Accuracy: 0.9926

# predict test set
pred_probability = model.predict(X_test_std)

# convert to bool
predictions = pred_probability > 0.5

# precision / recall / f1-score 
print(classification_report(y_test_std,predictions))

              precision    recall  f1-score   support

           0       1.00      1.00      1.00      1231
           1       0.99      0.99      0.99       394

    accuracy                           1.00      1625
   macro avg       0.99      1.00      0.99      1625
weighted avg       1.00      1.00      1.00      1625

plt.figure(figsize=(10,6))
sns.heatmap(confusion_matrix(y_test_std,predictions),annot=True)

<matplotlib.axes._subplots.AxesSubplot at 0x7f4c3c439c90>

2.4 Multi-Class Classification

back to top

It is good practice, and often necessary to one-hot encode the target values for a multi-class problem. We will need to do that with our wine data here.

🏋️ Exercise 3: Multi-Class Classification

1) Define Model

Define a model with both batch normalization and dropout layers.

2) Add Optimizer, Loss, and Metric

3) Train and Evaluate

from keras.utils import np_utils

wine = pd.read_csv("https://raw.githubusercontent.com/wesleybeckner/"\
      "ds_for_engineers/main/data/wine_quality/winequalityN.csv")

# create X and y
X = wine.copy()
y = X.pop('quality')

# preprocess y for quality and/or type
encoder = LabelEncoder()
encoder.fit(y)
encoded_y = encoder.transform(y)
y = np_utils.to_categorical(encoded_y)

# split into train/test
X_train, X_test, y_train, y_test = train_test_split(X, y)
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train)

# the numerical values pipe
num_proc = make_pipeline(SimpleImputer(strategy='median'), StandardScaler())

# the categorical values pipe
cat_proc = make_pipeline(
    SimpleImputer(strategy='constant', fill_value='missing'),
    OneHotEncoder(handle_unknown='ignore'))

# parallelize the two pipes
preprocessor = make_column_transformer((num_proc,
                                make_column_selector(dtype_include=np.number)),
                                       (cat_proc,
                                make_column_selector(dtype_include=object)))

X_train_std = preprocessor.fit_transform(X_train) # fit_transform on train
X_test_std = preprocessor.transform(X_test) # transform test
X_val_std = preprocessor.transform(X_val)

y_train_std = y_train
y_val_std = y_val
y_test_std = y_test

preprocessor

ColumnTransformer

ColumnTransformer(transformers=[('pipeline-1',
                                 Pipeline(steps=[('simpleimputer',
                                                  SimpleImputer(strategy='median')),
                                                 ('standardscaler',
                                                  StandardScaler())]),
                                 ),
                                ('pipeline-2',
                                 Pipeline(steps=[('simpleimputer',
                                                  SimpleImputer(fill_value='missing',
                                                                strategy='constant')),
                                                 ('onehotencoder',
                                                  OneHotEncoder(handle_unknown='ignore'))]),
                                 )])

pipeline-1

SimpleImputer

SimpleImputer(strategy='median')

StandardScaler

StandardScaler()

pipeline-2

SimpleImputer

SimpleImputer(fill_value='missing', strategy='constant')

OneHotEncoder

OneHotEncoder(handle_unknown='ignore')

from tensorflow import keras
from tensorflow.keras import layers

model = keras.Sequential([
  ### YOUR MODEL HERE ###
])

print(model.summary())

Model: "sequential_8"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_33 (Dense)             (None, 4)                 56        
_________________________________________________________________
dense_34 (Dense)             (None, 4)                 20        
_________________________________________________________________
dense_35 (Dense)             (None, 7)                 35        
=================================================================
Total params: 111
Trainable params: 111
Non-trainable params: 0
_________________________________________________________________
None

model.compile(
    optimizer='adam',
    loss='categorical_crossentropy',
    metrics=['accuracy'],
)

early_stopping = keras.callbacks.EarlyStopping(
    patience=10,
    min_delta=0.001,
    restore_best_weights=True,
)

history = model.fit(
    X_train_std, y_train_std,
    validation_data=(X_val_std, y_val_std),
    batch_size=512,
    epochs=1000,
    callbacks=[early_stopping],
    verbose=1, # hide the output because we have so many epochs
)

Epoch 1/1000
8/8 [==============================] - 1s 25ms/step - loss: 1.9526 - accuracy: 0.1089 - val_loss: 1.9443 - val_accuracy: 0.1667
Epoch 2/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.9330 - accuracy: 0.1656 - val_loss: 1.9251 - val_accuracy: 0.2192
Epoch 3/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.9144 - accuracy: 0.2288 - val_loss: 1.9066 - val_accuracy: 0.3005
Epoch 4/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.8962 - accuracy: 0.3049 - val_loss: 1.8879 - val_accuracy: 0.3259
Epoch 5/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.8778 - accuracy: 0.3309 - val_loss: 1.8686 - val_accuracy: 0.3563
Epoch 6/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.8586 - accuracy: 0.3629 - val_loss: 1.8485 - val_accuracy: 0.3834
Epoch 7/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.8387 - accuracy: 0.3829 - val_loss: 1.8270 - val_accuracy: 0.4015
Epoch 8/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.8174 - accuracy: 0.3960 - val_loss: 1.8045 - val_accuracy: 0.4097
Epoch 9/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.7950 - accuracy: 0.4056 - val_loss: 1.7808 - val_accuracy: 0.4146
Epoch 10/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.7713 - accuracy: 0.4146 - val_loss: 1.7556 - val_accuracy: 0.4220
Epoch 11/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.7465 - accuracy: 0.4187 - val_loss: 1.7291 - val_accuracy: 0.4220
Epoch 12/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.7204 - accuracy: 0.4220 - val_loss: 1.7017 - val_accuracy: 0.4245
Epoch 13/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.6936 - accuracy: 0.4245 - val_loss: 1.6735 - val_accuracy: 0.4245
Epoch 14/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.6663 - accuracy: 0.4261 - val_loss: 1.6452 - val_accuracy: 0.4294
Epoch 15/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.6390 - accuracy: 0.4302 - val_loss: 1.6171 - val_accuracy: 0.4261
Epoch 16/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.6114 - accuracy: 0.4335 - val_loss: 1.5890 - val_accuracy: 0.4310
Epoch 17/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.5836 - accuracy: 0.4387 - val_loss: 1.5613 - val_accuracy: 0.4286
Epoch 18/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.5562 - accuracy: 0.4417 - val_loss: 1.5347 - val_accuracy: 0.4319
Epoch 19/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.5300 - accuracy: 0.4469 - val_loss: 1.5096 - val_accuracy: 0.4376
Epoch 20/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.5058 - accuracy: 0.4518 - val_loss: 1.4865 - val_accuracy: 0.4433
Epoch 21/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.4831 - accuracy: 0.4559 - val_loss: 1.4651 - val_accuracy: 0.4442
Epoch 22/1000
8/8 [==============================] - 0s 8ms/step - loss: 1.4626 - accuracy: 0.4570 - val_loss: 1.4460 - val_accuracy: 0.4466
Epoch 23/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.4440 - accuracy: 0.4576 - val_loss: 1.4287 - val_accuracy: 0.4507
Epoch 24/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.4274 - accuracy: 0.4592 - val_loss: 1.4126 - val_accuracy: 0.4507
Epoch 25/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.4120 - accuracy: 0.4587 - val_loss: 1.3978 - val_accuracy: 0.4548
Epoch 26/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.3984 - accuracy: 0.4589 - val_loss: 1.3841 - val_accuracy: 0.4548
Epoch 27/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.3859 - accuracy: 0.4617 - val_loss: 1.3713 - val_accuracy: 0.4548
Epoch 28/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.3744 - accuracy: 0.4603 - val_loss: 1.3598 - val_accuracy: 0.4532
Epoch 29/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.3640 - accuracy: 0.4625 - val_loss: 1.3494 - val_accuracy: 0.4565
Epoch 30/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.3545 - accuracy: 0.4636 - val_loss: 1.3401 - val_accuracy: 0.4581
Epoch 31/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.3459 - accuracy: 0.4641 - val_loss: 1.3317 - val_accuracy: 0.4581
Epoch 32/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.3380 - accuracy: 0.4641 - val_loss: 1.3236 - val_accuracy: 0.4573
Epoch 33/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.3310 - accuracy: 0.4636 - val_loss: 1.3165 - val_accuracy: 0.4565
Epoch 34/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.3244 - accuracy: 0.4644 - val_loss: 1.3100 - val_accuracy: 0.4589
Epoch 35/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.3182 - accuracy: 0.4652 - val_loss: 1.3039 - val_accuracy: 0.4573
Epoch 36/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.3126 - accuracy: 0.4631 - val_loss: 1.2982 - val_accuracy: 0.4565
Epoch 37/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.3071 - accuracy: 0.4628 - val_loss: 1.2929 - val_accuracy: 0.4622
Epoch 38/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.3022 - accuracy: 0.4628 - val_loss: 1.2881 - val_accuracy: 0.4639
Epoch 39/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2976 - accuracy: 0.4639 - val_loss: 1.2838 - val_accuracy: 0.4647
Epoch 40/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2937 - accuracy: 0.4636 - val_loss: 1.2797 - val_accuracy: 0.4639
Epoch 41/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2897 - accuracy: 0.4639 - val_loss: 1.2758 - val_accuracy: 0.4639
Epoch 42/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2862 - accuracy: 0.4631 - val_loss: 1.2722 - val_accuracy: 0.4631
Epoch 43/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.2830 - accuracy: 0.4639 - val_loss: 1.2686 - val_accuracy: 0.4614
Epoch 44/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2798 - accuracy: 0.4636 - val_loss: 1.2658 - val_accuracy: 0.4614
Epoch 45/1000
8/8 [==============================] - 0s 7ms/step - loss: 1.2768 - accuracy: 0.4644 - val_loss: 1.2631 - val_accuracy: 0.4639
Epoch 46/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2740 - accuracy: 0.4661 - val_loss: 1.2608 - val_accuracy: 0.4647
Epoch 47/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2712 - accuracy: 0.4658 - val_loss: 1.2582 - val_accuracy: 0.4647
Epoch 48/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2686 - accuracy: 0.4661 - val_loss: 1.2559 - val_accuracy: 0.4672
Epoch 49/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2657 - accuracy: 0.4680 - val_loss: 1.2529 - val_accuracy: 0.4713
Epoch 50/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2631 - accuracy: 0.4669 - val_loss: 1.2500 - val_accuracy: 0.4713
Epoch 51/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2606 - accuracy: 0.4688 - val_loss: 1.2470 - val_accuracy: 0.4778
Epoch 52/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.2580 - accuracy: 0.4735 - val_loss: 1.2438 - val_accuracy: 0.4811
Epoch 53/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.2556 - accuracy: 0.4726 - val_loss: 1.2408 - val_accuracy: 0.4860
Epoch 54/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.2530 - accuracy: 0.4751 - val_loss: 1.2377 - val_accuracy: 0.4852
Epoch 55/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.2502 - accuracy: 0.4770 - val_loss: 1.2358 - val_accuracy: 0.4901
Epoch 56/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2477 - accuracy: 0.4781 - val_loss: 1.2343 - val_accuracy: 0.4885
Epoch 57/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2451 - accuracy: 0.4787 - val_loss: 1.2317 - val_accuracy: 0.4926
Epoch 58/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2422 - accuracy: 0.4825 - val_loss: 1.2286 - val_accuracy: 0.4959
Epoch 59/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2396 - accuracy: 0.4828 - val_loss: 1.2265 - val_accuracy: 0.4992
Epoch 60/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2371 - accuracy: 0.4839 - val_loss: 1.2242 - val_accuracy: 0.5000
Epoch 61/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2342 - accuracy: 0.4839 - val_loss: 1.2221 - val_accuracy: 0.4967
Epoch 62/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.2313 - accuracy: 0.4877 - val_loss: 1.2200 - val_accuracy: 0.4967
Epoch 63/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2287 - accuracy: 0.4893 - val_loss: 1.2178 - val_accuracy: 0.5025
Epoch 64/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.2262 - accuracy: 0.4891 - val_loss: 1.2158 - val_accuracy: 0.5016
Epoch 65/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2237 - accuracy: 0.4915 - val_loss: 1.2135 - val_accuracy: 0.5016
Epoch 66/1000
8/8 [==============================] - 0s 8ms/step - loss: 1.2213 - accuracy: 0.4918 - val_loss: 1.2119 - val_accuracy: 0.5025
Epoch 67/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2189 - accuracy: 0.4926 - val_loss: 1.2100 - val_accuracy: 0.5000
Epoch 68/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2166 - accuracy: 0.4951 - val_loss: 1.2072 - val_accuracy: 0.5074
Epoch 69/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2137 - accuracy: 0.4973 - val_loss: 1.2052 - val_accuracy: 0.5025
Epoch 70/1000
8/8 [==============================] - 0s 7ms/step - loss: 1.2114 - accuracy: 0.4995 - val_loss: 1.2028 - val_accuracy: 0.5025
Epoch 71/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2088 - accuracy: 0.5003 - val_loss: 1.1996 - val_accuracy: 0.5041
Epoch 72/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2062 - accuracy: 0.5019 - val_loss: 1.1964 - val_accuracy: 0.5066
Epoch 73/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.2036 - accuracy: 0.5027 - val_loss: 1.1936 - val_accuracy: 0.5049
Epoch 74/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.2013 - accuracy: 0.5055 - val_loss: 1.1917 - val_accuracy: 0.5082
Epoch 75/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1988 - accuracy: 0.5041 - val_loss: 1.1900 - val_accuracy: 0.5057
Epoch 76/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1959 - accuracy: 0.5038 - val_loss: 1.1879 - val_accuracy: 0.5099
Epoch 77/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1934 - accuracy: 0.5049 - val_loss: 1.1854 - val_accuracy: 0.5131
Epoch 78/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1908 - accuracy: 0.5077 - val_loss: 1.1830 - val_accuracy: 0.5107
Epoch 79/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1879 - accuracy: 0.5071 - val_loss: 1.1810 - val_accuracy: 0.5074
Epoch 80/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1852 - accuracy: 0.5060 - val_loss: 1.1786 - val_accuracy: 0.5074
Epoch 81/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1824 - accuracy: 0.5082 - val_loss: 1.1767 - val_accuracy: 0.5090
Epoch 82/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1798 - accuracy: 0.5093 - val_loss: 1.1743 - val_accuracy: 0.5066
Epoch 83/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1774 - accuracy: 0.5093 - val_loss: 1.1719 - val_accuracy: 0.5041
Epoch 84/1000
8/8 [==============================] - 0s 7ms/step - loss: 1.1749 - accuracy: 0.5088 - val_loss: 1.1693 - val_accuracy: 0.5066
Epoch 85/1000
8/8 [==============================] - 0s 7ms/step - loss: 1.1721 - accuracy: 0.5099 - val_loss: 1.1665 - val_accuracy: 0.5140
Epoch 86/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1696 - accuracy: 0.5112 - val_loss: 1.1640 - val_accuracy: 0.5189
Epoch 87/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1674 - accuracy: 0.5129 - val_loss: 1.1616 - val_accuracy: 0.5197
Epoch 88/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1649 - accuracy: 0.5126 - val_loss: 1.1597 - val_accuracy: 0.5172
Epoch 89/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1625 - accuracy: 0.5142 - val_loss: 1.1580 - val_accuracy: 0.5172
Epoch 90/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1601 - accuracy: 0.5142 - val_loss: 1.1562 - val_accuracy: 0.5148
Epoch 91/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1579 - accuracy: 0.5153 - val_loss: 1.1543 - val_accuracy: 0.5156
Epoch 92/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1557 - accuracy: 0.5142 - val_loss: 1.1526 - val_accuracy: 0.5181
Epoch 93/1000
8/8 [==============================] - 0s 7ms/step - loss: 1.1534 - accuracy: 0.5140 - val_loss: 1.1515 - val_accuracy: 0.5172
Epoch 94/1000
8/8 [==============================] - 0s 8ms/step - loss: 1.1514 - accuracy: 0.5151 - val_loss: 1.1505 - val_accuracy: 0.5156
Epoch 95/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1494 - accuracy: 0.5151 - val_loss: 1.1489 - val_accuracy: 0.5115
Epoch 96/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1475 - accuracy: 0.5170 - val_loss: 1.1475 - val_accuracy: 0.5172
Epoch 97/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1453 - accuracy: 0.5189 - val_loss: 1.1452 - val_accuracy: 0.5148
Epoch 98/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1430 - accuracy: 0.5192 - val_loss: 1.1430 - val_accuracy: 0.5148
Epoch 99/1000
8/8 [==============================] - 0s 7ms/step - loss: 1.1410 - accuracy: 0.5186 - val_loss: 1.1409 - val_accuracy: 0.5148
Epoch 100/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1391 - accuracy: 0.5208 - val_loss: 1.1392 - val_accuracy: 0.5164
Epoch 101/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1374 - accuracy: 0.5205 - val_loss: 1.1380 - val_accuracy: 0.5197
Epoch 102/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1357 - accuracy: 0.5235 - val_loss: 1.1369 - val_accuracy: 0.5156
Epoch 103/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1338 - accuracy: 0.5244 - val_loss: 1.1354 - val_accuracy: 0.5156
Epoch 104/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1322 - accuracy: 0.5241 - val_loss: 1.1349 - val_accuracy: 0.5172
Epoch 105/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1303 - accuracy: 0.5227 - val_loss: 1.1331 - val_accuracy: 0.5181
Epoch 106/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1285 - accuracy: 0.5257 - val_loss: 1.1311 - val_accuracy: 0.5189
Epoch 107/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1268 - accuracy: 0.5276 - val_loss: 1.1298 - val_accuracy: 0.5181
Epoch 108/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1249 - accuracy: 0.5315 - val_loss: 1.1287 - val_accuracy: 0.5238
Epoch 109/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1232 - accuracy: 0.5353 - val_loss: 1.1271 - val_accuracy: 0.5271
Epoch 110/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1217 - accuracy: 0.5372 - val_loss: 1.1254 - val_accuracy: 0.5255
Epoch 111/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1201 - accuracy: 0.5397 - val_loss: 1.1235 - val_accuracy: 0.5312
Epoch 112/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1183 - accuracy: 0.5397 - val_loss: 1.1224 - val_accuracy: 0.5312
Epoch 113/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1167 - accuracy: 0.5416 - val_loss: 1.1213 - val_accuracy: 0.5304
Epoch 114/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1152 - accuracy: 0.5449 - val_loss: 1.1202 - val_accuracy: 0.5312
Epoch 115/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1136 - accuracy: 0.5457 - val_loss: 1.1189 - val_accuracy: 0.5328
Epoch 116/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1117 - accuracy: 0.5468 - val_loss: 1.1179 - val_accuracy: 0.5353
Epoch 117/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1103 - accuracy: 0.5471 - val_loss: 1.1175 - val_accuracy: 0.5353
Epoch 118/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1089 - accuracy: 0.5465 - val_loss: 1.1171 - val_accuracy: 0.5345
Epoch 119/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1075 - accuracy: 0.5471 - val_loss: 1.1165 - val_accuracy: 0.5378
Epoch 120/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1062 - accuracy: 0.5487 - val_loss: 1.1153 - val_accuracy: 0.5411
Epoch 121/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1049 - accuracy: 0.5498 - val_loss: 1.1142 - val_accuracy: 0.5378
Epoch 122/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.1036 - accuracy: 0.5501 - val_loss: 1.1134 - val_accuracy: 0.5312
Epoch 123/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1024 - accuracy: 0.5484 - val_loss: 1.1121 - val_accuracy: 0.5353
Epoch 124/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1011 - accuracy: 0.5501 - val_loss: 1.1115 - val_accuracy: 0.5402
Epoch 125/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.1000 - accuracy: 0.5523 - val_loss: 1.1109 - val_accuracy: 0.5411
Epoch 126/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0987 - accuracy: 0.5506 - val_loss: 1.1092 - val_accuracy: 0.5378
Epoch 127/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0972 - accuracy: 0.5561 - val_loss: 1.1080 - val_accuracy: 0.5361
Epoch 128/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0958 - accuracy: 0.5534 - val_loss: 1.1080 - val_accuracy: 0.5337
Epoch 129/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0947 - accuracy: 0.5558 - val_loss: 1.1077 - val_accuracy: 0.5353
Epoch 130/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0933 - accuracy: 0.5531 - val_loss: 1.1074 - val_accuracy: 0.5369
Epoch 131/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0922 - accuracy: 0.5536 - val_loss: 1.1070 - val_accuracy: 0.5394
Epoch 132/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0911 - accuracy: 0.5523 - val_loss: 1.1059 - val_accuracy: 0.5394
Epoch 133/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0900 - accuracy: 0.5536 - val_loss: 1.1047 - val_accuracy: 0.5378
Epoch 134/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0890 - accuracy: 0.5545 - val_loss: 1.1034 - val_accuracy: 0.5411
Epoch 135/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0879 - accuracy: 0.5564 - val_loss: 1.1017 - val_accuracy: 0.5427
Epoch 136/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0869 - accuracy: 0.5545 - val_loss: 1.1010 - val_accuracy: 0.5435
Epoch 137/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0860 - accuracy: 0.5564 - val_loss: 1.1006 - val_accuracy: 0.5435
Epoch 138/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0849 - accuracy: 0.5567 - val_loss: 1.1004 - val_accuracy: 0.5443
Epoch 139/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0842 - accuracy: 0.5553 - val_loss: 1.0999 - val_accuracy: 0.5452
Epoch 140/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0831 - accuracy: 0.5558 - val_loss: 1.0988 - val_accuracy: 0.5484
Epoch 141/1000
8/8 [==============================] - 0s 7ms/step - loss: 1.0822 - accuracy: 0.5550 - val_loss: 1.0979 - val_accuracy: 0.5525
Epoch 142/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0816 - accuracy: 0.5577 - val_loss: 1.0975 - val_accuracy: 0.5493
Epoch 143/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0809 - accuracy: 0.5556 - val_loss: 1.0971 - val_accuracy: 0.5517
Epoch 144/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0800 - accuracy: 0.5545 - val_loss: 1.0970 - val_accuracy: 0.5484
Epoch 145/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0792 - accuracy: 0.5545 - val_loss: 1.0964 - val_accuracy: 0.5493
Epoch 146/1000
8/8 [==============================] - 0s 7ms/step - loss: 1.0785 - accuracy: 0.5572 - val_loss: 1.0956 - val_accuracy: 0.5517
Epoch 147/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0777 - accuracy: 0.5569 - val_loss: 1.0943 - val_accuracy: 0.5517
Epoch 148/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0771 - accuracy: 0.5586 - val_loss: 1.0937 - val_accuracy: 0.5542
Epoch 149/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0764 - accuracy: 0.5588 - val_loss: 1.0930 - val_accuracy: 0.5542
Epoch 150/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0759 - accuracy: 0.5586 - val_loss: 1.0926 - val_accuracy: 0.5599
Epoch 151/1000
8/8 [==============================] - 0s 8ms/step - loss: 1.0756 - accuracy: 0.5580 - val_loss: 1.0926 - val_accuracy: 0.5575
Epoch 152/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0750 - accuracy: 0.5577 - val_loss: 1.0926 - val_accuracy: 0.5567
Epoch 153/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0743 - accuracy: 0.5564 - val_loss: 1.0926 - val_accuracy: 0.5534
Epoch 154/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0736 - accuracy: 0.5569 - val_loss: 1.0918 - val_accuracy: 0.5525
Epoch 155/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0732 - accuracy: 0.5577 - val_loss: 1.0912 - val_accuracy: 0.5558
Epoch 156/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0727 - accuracy: 0.5567 - val_loss: 1.0906 - val_accuracy: 0.5567
Epoch 157/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0724 - accuracy: 0.5577 - val_loss: 1.0908 - val_accuracy: 0.5525
Epoch 158/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0720 - accuracy: 0.5553 - val_loss: 1.0906 - val_accuracy: 0.5534
Epoch 159/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0715 - accuracy: 0.5561 - val_loss: 1.0903 - val_accuracy: 0.5525
Epoch 160/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0710 - accuracy: 0.5556 - val_loss: 1.0897 - val_accuracy: 0.5534
Epoch 161/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0706 - accuracy: 0.5558 - val_loss: 1.0887 - val_accuracy: 0.5525
Epoch 162/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0704 - accuracy: 0.5577 - val_loss: 1.0883 - val_accuracy: 0.5542
Epoch 163/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0700 - accuracy: 0.5564 - val_loss: 1.0882 - val_accuracy: 0.5534
Epoch 164/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0697 - accuracy: 0.5553 - val_loss: 1.0880 - val_accuracy: 0.5558
Epoch 165/1000
8/8 [==============================] - 0s 7ms/step - loss: 1.0694 - accuracy: 0.5553 - val_loss: 1.0879 - val_accuracy: 0.5534
Epoch 166/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0693 - accuracy: 0.5558 - val_loss: 1.0880 - val_accuracy: 0.5550
Epoch 167/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0690 - accuracy: 0.5569 - val_loss: 1.0876 - val_accuracy: 0.5567
Epoch 168/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0685 - accuracy: 0.5550 - val_loss: 1.0871 - val_accuracy: 0.5575
Epoch 169/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0684 - accuracy: 0.5564 - val_loss: 1.0873 - val_accuracy: 0.5599
Epoch 170/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0679 - accuracy: 0.5558 - val_loss: 1.0867 - val_accuracy: 0.5567
Epoch 171/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0679 - accuracy: 0.5577 - val_loss: 1.0871 - val_accuracy: 0.5575
Epoch 172/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0673 - accuracy: 0.5575 - val_loss: 1.0865 - val_accuracy: 0.5542
Epoch 173/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0670 - accuracy: 0.5556 - val_loss: 1.0866 - val_accuracy: 0.5591
Epoch 174/1000
8/8 [==============================] - 0s 8ms/step - loss: 1.0665 - accuracy: 0.5539 - val_loss: 1.0862 - val_accuracy: 0.5583
Epoch 175/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0662 - accuracy: 0.5547 - val_loss: 1.0862 - val_accuracy: 0.5599
Epoch 176/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0659 - accuracy: 0.5556 - val_loss: 1.0857 - val_accuracy: 0.5583
Epoch 177/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0654 - accuracy: 0.5539 - val_loss: 1.0851 - val_accuracy: 0.5558
Epoch 178/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0652 - accuracy: 0.5542 - val_loss: 1.0841 - val_accuracy: 0.5575
Epoch 179/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0650 - accuracy: 0.5523 - val_loss: 1.0840 - val_accuracy: 0.5575
Epoch 180/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0647 - accuracy: 0.5534 - val_loss: 1.0834 - val_accuracy: 0.5534
Epoch 181/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0644 - accuracy: 0.5553 - val_loss: 1.0833 - val_accuracy: 0.5542
Epoch 182/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0641 - accuracy: 0.5534 - val_loss: 1.0832 - val_accuracy: 0.5542
Epoch 183/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0637 - accuracy: 0.5539 - val_loss: 1.0835 - val_accuracy: 0.5575
Epoch 184/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0636 - accuracy: 0.5550 - val_loss: 1.0839 - val_accuracy: 0.5599
Epoch 185/1000
8/8 [==============================] - 0s 8ms/step - loss: 1.0634 - accuracy: 0.5506 - val_loss: 1.0837 - val_accuracy: 0.5575
Epoch 186/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0634 - accuracy: 0.5501 - val_loss: 1.0826 - val_accuracy: 0.5517
Epoch 187/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0634 - accuracy: 0.5534 - val_loss: 1.0823 - val_accuracy: 0.5542
Epoch 188/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0631 - accuracy: 0.5517 - val_loss: 1.0820 - val_accuracy: 0.5534
Epoch 189/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0626 - accuracy: 0.5528 - val_loss: 1.0822 - val_accuracy: 0.5558
Epoch 190/1000
8/8 [==============================] - 0s 7ms/step - loss: 1.0626 - accuracy: 0.5495 - val_loss: 1.0824 - val_accuracy: 0.5575
Epoch 191/1000
8/8 [==============================] - 0s 7ms/step - loss: 1.0623 - accuracy: 0.5523 - val_loss: 1.0818 - val_accuracy: 0.5599
Epoch 192/1000
8/8 [==============================] - 0s 7ms/step - loss: 1.0621 - accuracy: 0.5542 - val_loss: 1.0817 - val_accuracy: 0.5575
Epoch 193/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0618 - accuracy: 0.5558 - val_loss: 1.0812 - val_accuracy: 0.5558
Epoch 194/1000
8/8 [==============================] - 0s 7ms/step - loss: 1.0619 - accuracy: 0.5553 - val_loss: 1.0812 - val_accuracy: 0.5575
Epoch 195/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0617 - accuracy: 0.5564 - val_loss: 1.0813 - val_accuracy: 0.5567
Epoch 196/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0614 - accuracy: 0.5547 - val_loss: 1.0810 - val_accuracy: 0.5624
Epoch 197/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0613 - accuracy: 0.5531 - val_loss: 1.0812 - val_accuracy: 0.5640
Epoch 198/1000
8/8 [==============================] - 0s 9ms/step - loss: 1.0613 - accuracy: 0.5536 - val_loss: 1.0817 - val_accuracy: 0.5649
Epoch 199/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0611 - accuracy: 0.5520 - val_loss: 1.0817 - val_accuracy: 0.5640
Epoch 200/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0610 - accuracy: 0.5509 - val_loss: 1.0815 - val_accuracy: 0.5632
Epoch 201/1000
8/8 [==============================] - 0s 5ms/step - loss: 1.0606 - accuracy: 0.5506 - val_loss: 1.0812 - val_accuracy: 0.5640
Epoch 202/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0606 - accuracy: 0.5487 - val_loss: 1.0814 - val_accuracy: 0.5599
Epoch 203/1000
8/8 [==============================] - 0s 6ms/step - loss: 1.0606 - accuracy: 0.5515 - val_loss: 1.0807 - val_accuracy: 0.5599

history_df = pd.DataFrame(history.history)

history_df.loc[:, ['loss', 'val_loss']].plot()
history_df.loc[:, ['accuracy', 'val_accuracy']].plot()

print(("Best Validation Loss: {:0.4f}" +\
      "\nBest Validation Accuracy: {:0.4f}")\
      .format(history_df['val_loss'].min(), 
              history_df['val_accuracy'].max()))

Best Validation Loss: 1.0807
Best Validation Accuracy: 0.5649

# predict test set
pred_probability = model.predict(X_test_std)

# convert to bool
predictions = pred_probability > 0.5

# precision / recall / f1-score 
print(classification_report(y_test_std,predictions))

              precision    recall  f1-score   support

           0       0.06      0.22      0.09         9
           1       0.06      0.78      0.11        55
           2       0.36      0.99      0.53       535
           3       0.43      1.00      0.60       698
           4       0.19      1.00      0.31       286
           5       0.05      0.85      0.09        41
           6       0.00      0.00      0.00         1

   micro avg       0.26      0.98      0.41      1625
   macro avg       0.16      0.69      0.25      1625
weighted avg       0.34      0.98      0.49      1625
 samples avg       0.26      0.98      0.41      1625



/usr/local/lib/python3.7/dist-packages/sklearn/metrics/_classification.py:1248: UndefinedMetricWarning: Precision and F-score are ill-defined and being set to 0.0 in labels with no predicted samples. Use `zero_division` parameter to control this behavior.
  _warn_prf(average, modifier, msg_start, len(result))

References

Difference between a batch and an epoch

Cross Entropy